ゲーム数を増やすことで結果を安定させる
このページで検証したように、たとえボーダーを上回る釘調整の台でも、2,000回転程度のゲーム数では安定した結果は得られない。結果を安定させるには台数と打ち手の人数、回転数を増やすしかない。
逆に、店側はボーダーを下回る釘にしておけば、個々の台の出玉のバラつきはともかく、全台の合計値としてはプラスの結果を得られる確率が非常に高くなる。
結論としては十分に甘い釘の台をできるだけ多く占有できれば、釘の甘さと占有した台数に応じて、それなりの勝率を得ることができる。
ただし、優良台を占拠する作戦で大金持ちになることは難しい。
パチンコ店の営業時間と1玉の価値には上限あり、利益にも限界があるためだ。
また、軍団を組織する行動力や組織力があるなら、それは別の分野で生かしたほうが高い収益を得られるのではないかとも思われる。
この考え方をシミュレーターで検証する。
20回転/1Kのリゼロ2を10台占有できたら
1台あたり2,000ゲーム、これを10台分合計した結果がどの程度安定するのか検証する。
2,000回転x10台x10万セット(20億回転)も試行しただけあって、きれいな分布図が得られた。
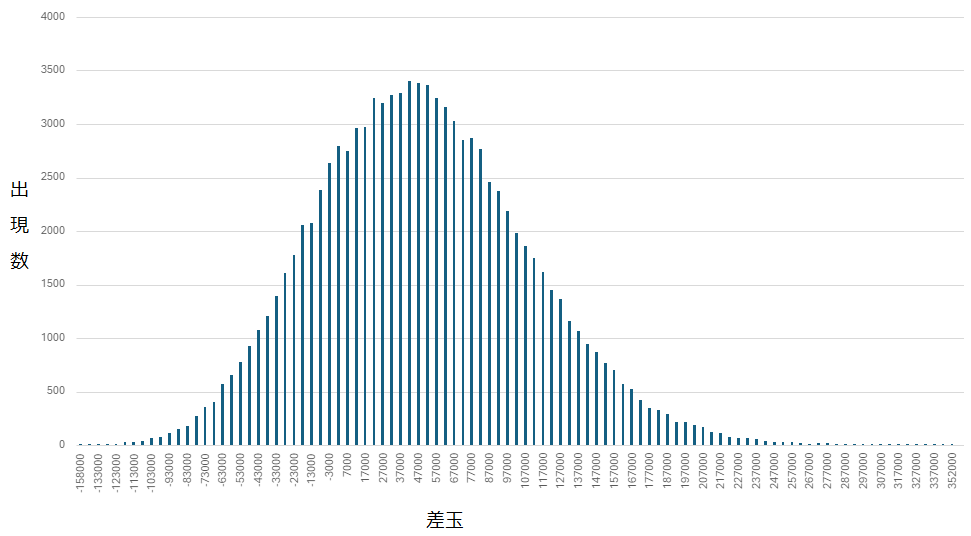
<2,000回転x10台分の合計>
平均:+49760玉
標準偏差:59907
マイナス域:20%
プラス域:80%
結果としては、平均でプラス5万玉近い差玉が得られることが分かった。
2,000ゲーム試行時の平均値は+4,924玉だったので、10台分にすれば平均値が約10倍になるのは当然であるが、勝率は50%強から80%にアップする(試行回数の増加によって結果が安定する)。
打ち子に対していくら日当を払えるか
20回転/1Kの台を10台確保できた場合の期待値は20万近くであることが分かった。
打ち子の日当を1人1万円とすると、元締めの利益の期待値は10万。
ただし、ひとまず換金ロスを無視しても、10人に日当を支払える差玉+25,000発以上の割合は約64%。
10人の打ち子に1万円の日当を支払うなら、ここが最低ラインである。
残りの36%は日当を支払ったら赤字である。
そもそも20回転/1Kも回る台をそこまで大量かつ頻繁に確保するのも大変だろうから、
軍団も楽な稼業ではないと考えられる。
打ち子としても、日当1万では時給は800円だ。
本来、20回転/1Kのリゼロなら2万/日の期待値がある。
これを日当1万で打つということは、不確実な期待値2万よりも確実な時給800円を選ぶことである。
もし打ち子に2万の日当を支払ったら期待値はゼロ、勝率ほぼ5割、標準偏差24万円のギャンブルを打つのと同じことになるので、日当2万を支払える元締めはいないだろう。
あとは登録料とか罰金などの名目で、元締めが打ち子から金を吸い上げる方式だが、
これについては本サイトの趣旨である確率計算や統計から外れることなので知らん。



コメント