回転ムラとは
意外と考察されることが少ないパチンコの回転ムラ。
同じところを狙って打ち出したのに、なぜ1,000円当たりのスタートチャッカー入賞数は安定しないのだろうか。
最初の1,000円では10回しか回らなかったのに、次の1,000円では25回も回ったり。
このページでは回転ムラの発生原因や傾向を考察する。
回転ムラの発生原因
回転ムラの原因は次の2点だ。
・1玉ごとの打ち出し強度にわずかな差異が生じること
・打ち出しからスタートチャッカーまでの間に多数の釘などがあること
初期値のわずかな差異が結果に大きく反映する性質を「初期鋭敏性」という。パチンコの玉の軌道においては、玉の打ち出し強度が1%変化するだけで、最終的な玉の到達先がスタートチャッカーになったり、遠く離れた外れ穴になったりすることだ。
可動式のステージなどはともかく、盤面の釘の配置や角度は不動なのだから、完全に同じ強度で玉を打ち出せば玉は決定論的に動く。それなら、スタートチャッカーに至る打ち出し強度で打ち続ければ、すべての玉がスタートチャッカーに入ることになるが、決してそうはならない。
打ち出し強度はほとんど変化していないはずなのに、外れ玉はスタートチャッカーの近くに落ちるどころか、遠く離れた場所に飛ばされる。
これはハンドルを完全に固定したとしても、打ち出し強度がわずかに変化することによる結果である。
この打ち出し強度のわずかな差が、複数回の釘への接触によって、玉の到達位置に大きな差をもたらす。
回転ムラを確率的事象として考えてみる1(ボーダー回転数の場合)
打ち出し強度の乱れがランダムに発生するものであるとすると、スタートチャッカーへの入賞は確率的に発生する事象であるとみなせる。これをシミュレートして250玉あたりの回転ムラがどの程度になるのか、標準偏差を求める。
<前提>
・15玉に1玉の確率でスタートチャッカーに入賞する。
・ヘソ賞球は1。
・10,000セット試行
<結果>
1,000円(250玉)あたりの平均回転数:16.7回
標準偏差:4.258
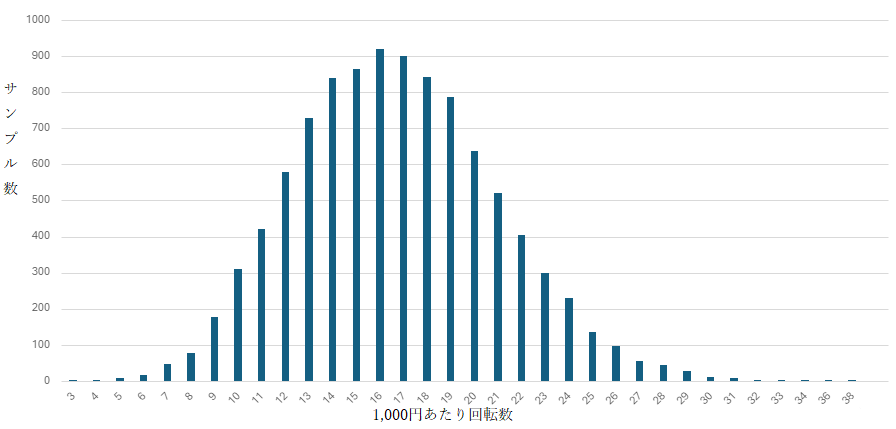
意外なことに、1万セットも試行しても1,000円で1回も回らないサンプルは得られなかった。
1/15でヘソに入賞することにしているので、1/15の事象を250回連続で外すのはさすがに無理であったということだ。
最低は3回転、最大は38回転(1サンプル)。
特に意図的な補正などは加えておらず、純粋にスタートチャッカーへの入賞を、確率的に発生する事象としてシミュレートした場合の分布である。
回転ムラを確率的事象として考えてみる2(厳しい釘調整の場合)
もう少し現実的に、1,000円で12~13回しか回らない場合の回転ムラを可視化してみる。
<前提>
・20玉に1玉の確率でスタートチャッカーに入賞する。
・ヘソ賞球は1。
・10,000セット試行
<結果>
1,000円(250玉)あたりの平均回転数:12.49回
標準偏差:3.631
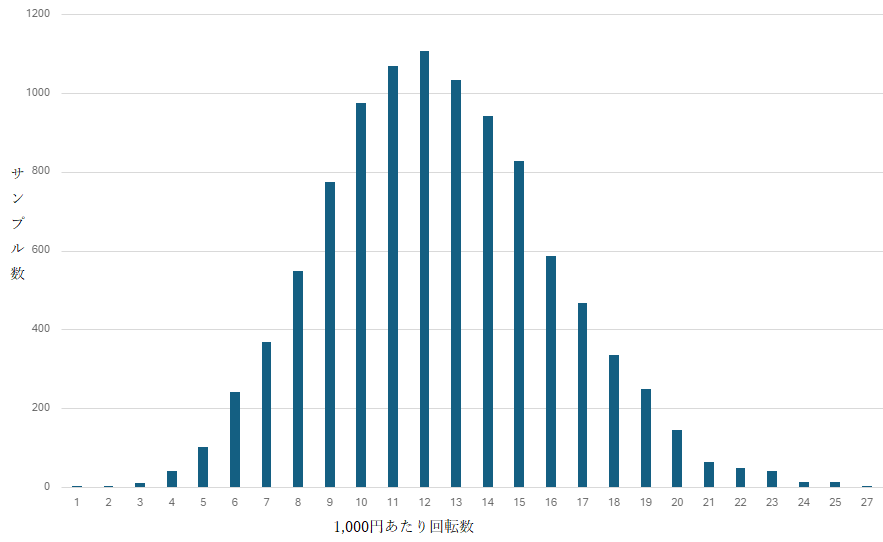
傾向は大差なく、これくらい厳しい釘調整でも0回転/1Kのサンプルは得られなかった。
1万円分打ち込めば回転数は安定するか?
■15玉に1回入賞する場合
平均:166.8回転
標準偏差:13.365
■20玉に1回入賞する場合
平均:125.0回転
標準偏差:11.448
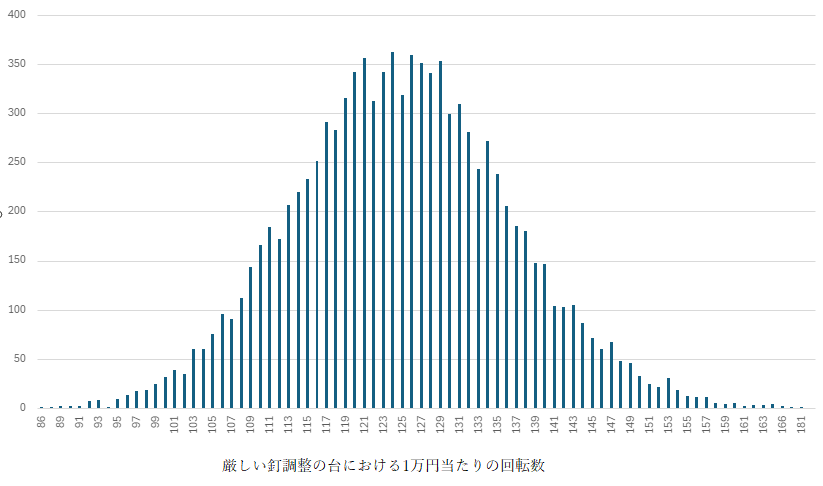
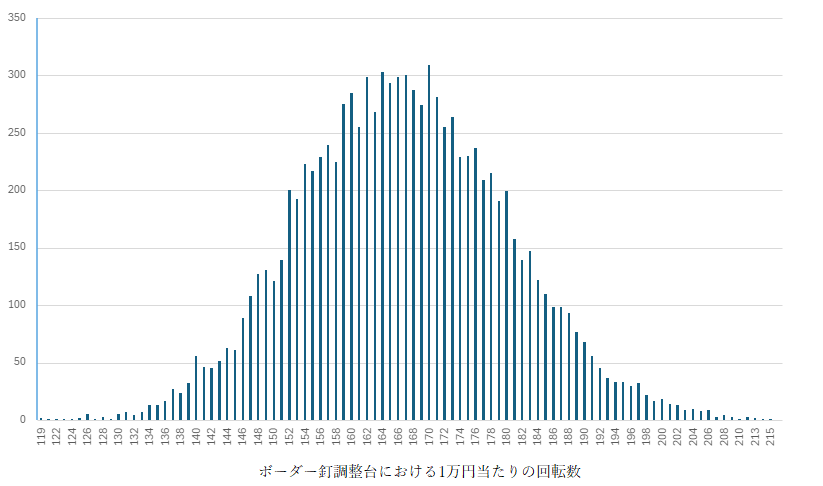
標準偏差は13や11なので、平均(166や125)を踏まえると、1万円ごとの集計では、
±10%程度の上振れや下振れは十分に発生し得る。ただし、±20%を超えるようなムラはめったに発生しないと言える。
この結果をどう応用すればよいかというと、最初の1万円でボーダーに20%以上足りない回数しか回らなかった場合、それが極めて不運であったか、よほどストロークが悪かったのでなければ、次の1万円でボーダーを上回る可能性は非常に低いということだ。
つまりそのような台はお金に余裕がある人以外は、新台初日だろうが即座にやめるべきだ。
1万円回して、ボーダーから20%以上少ない回転数しか回せなかった台はすぐにやめる。
ただし、ボーダーを上回るからと言って勝つ確率がそれほど高いわけではない。
上記の目安は収支ではなく、釘調整がボーダー以上かどうかを判断するためのものである点に注意されたい。
なお、10,000円使っても、1,000円あたり12回程度しか回らない台だと勝率は2割くらいしかないし、一日中打ち続けたら平均5万も負けるので即やめるように。




コメント